Wormholes Might be More Mirror-like Than Tunnel: Rethinking the Einstein-Rosen Bridge

Abstract

In January 2026, a theoretical upheaval emerged from the intersection of cosmology and quantum gravity, challenging nearly a century of assumptions regarding the topology of spacetime. A study published in Classical and Quantum Gravity by physicists Enrique Gaztañaga, K. Sravan Kumar, and João Marto proposed a radical reinterpretation of the Einstein-Rosen bridge.¹ Long relegated to the status of a "wormhole"—a theoretical tunnel for science fiction transit—the bridge is now posited as a fundamental "mirror" in spacetime, a necessary condition for the existence of quantum fields in curved geometries.³ This report provides an exhaustive, multi-disciplinary examination of this new framework, known as Direct-Sum Quantum Field Theory (DQFT). We explore the historical genesis of the bridge concept, the failure of standard quantum field theories at gravitational horizons, and the pivotal role of the Inverted Harmonic Oscillator (IHO) in modeling these interactions.⁴ Furthermore, we scrutinize the observational evidence identified in the Cosmic Microwave Background (CMB)—specifically, large-scale parity asymmetric features that favor this new model over standard inflationary cosmology by a statistical factor of 650.⁶ This analysis suggests that the unification of gravity and quantum mechanics requires acknowledging a universe that is a direct sum of two entangled, time-reversed sectors, fundamentally altering our understanding of time, entropy, and the origins of cosmic structure.

1. Introduction: The Persistence of the Bridge

The concept of the wormhole has occupied a paradoxical space in the human imagination for nearly one hundred years. It exists simultaneously as a staple of narrative fiction—a convenient plot device allowing instantaneous travel across the galaxy—and as a rigorously defined, albeit problematic, solution to the field equations of General Relativity. For decades, the gap between these two conceptions has been unbridgeable. The "wormholes" of fiction are stable and traversable; the "bridges" of relativity are unstable and impassable, collapsing before even a single photon can traverse the throat.

However, the dawn of 2026 has brought a shift in perspective that may be as significant as the original proposal of General Relativity itself. New research has suggested that we have fundamentally misunderstood the function of these bridges. They are not highways for matter, but channels for quantum information and consistency.⁸ The researchers argue that the Einstein-Rosen (ER) bridge represents a necessary condition for quantum fields to exist in curved spacetime without violating the principle of unitarity—the conservation of information.³

This paradigm shift is not merely a mathematical curiosity; it offers a potential resolution to some of the deepest crises in modern physics. The incompatibility of Quantum Mechanics (which governs the microscopic world) and General Relativity (which governs the macroscopic world) has plagued physicists since the 1930s. The new framework, Direct-Sum Quantum Field Theory (DQFT), suggests that this incompatibility arises from a "half-picture" of reality—a failure to account for a mirror-image sector of the universe where time flows backward at the microscopic scale.⁹

This report aims to deconstruct this complex theoretical development for the undergraduate student of physics and the interested academic observer. We will trace the lineage of the Einstein-Rosen bridge from its inception as a remedy for singularities to its modern reincarnation as a quantum stabilizer. We will delve into the mechanics of the "Inverted Harmonic Oscillator," a chaotic system that replaces the stable harmonic oscillator of standard quantum mechanics when dealing with gravitational horizons. We will also explore the profound connection between this physics and number theory, specifically the Riemann Hypothesis.⁴ Finally, we will present the "smoking gun" observational evidence: the discovery of parity asymmetry in the radiation left over from the Big Bang, a finding that suggests our universe is inextricably entangled with a mirror twin.

2. The Architecture of Spacetime: A Historical Reconstruction

To understand the magnitude of the recent reinterpretation, one must first grasp the architectural and conceptual origins of the bridge in General Relativity. The story begins not with a desire for travel, but with a hatred of singularities.

2.1 The Singularity Problem (1915–1935)

Following the formulation of General Relativity in 1915, Karl Schwarzschild provided the first exact solution to Einstein's field equations. This solution described the gravitational field of a spherical mass—what we now call a black hole. While mathematically brilliant, the solution contained a feature that Albert Einstein found physically abhorrent: a singularity. At the very center of the solution (r=0), the density of matter and the curvature of spacetime became infinite.

For Einstein, a singularity represented a breakdown of the theory. It was a place where the laws of physics ceased to function. Throughout the 1920s and 30s, Einstein sought a way to modify his theory or its solutions to eliminate these pathological points. He believed that a complete theory of nature should be free of singularities. This quest led him to collaborate with Nathan Rosen at the Institute for Advanced Study in Princeton.

In 1935, Einstein and Rosen published "The Particle Problem in General Relativity." Their goal was to construct a model of elementary particles that was purely geometric and free from singularities.¹ They achieved this by modifying the topology of the Schwarzschild solution.

2.2 The Construction of the Bridge

Einstein and Rosen realized that the singularity in the Schwarzschild metric was, in part, a product of the coordinate system used to describe it. By performing a specific coordinate transformation, they were able to map the region "inside" the horizon to a second, identical exterior region.

Imagine taking a sheet of paper (representing spacetime), poking a hole in it, and gluing a tube to the edges of the hole. Now, take a second sheet of paper, poke a corresponding hole, and glue the other end of the tube to it. You have created a bridge connecting two separate sheets.

In the Einstein-Rosen formulation, the "particle" was not a point of infinite density, but the "throat" of this bridge. If one were to travel toward the particle from one side, one would not hit a singularity; instead, one would pass through the throat and emerge into the other sheet of spacetime. This structure, the Einstein-Rosen (ER) bridge, successfully eliminated the central singularity. The "particle" was simply a manifestation of the topology of spacetime.¹

Crucially, Einstein and Rosen did not interpret this as a tunnel between two different universes in the science fiction sense. They viewed the two sheets as two parts of the same physical universe, connected by the bridge. The bridge was a model for an elementary particle, like an electron or a proton, which possessed mass and charge solely due to the geometric curvature of the throat.

2.3 The Wheeler Era and the "Wormhole"

The concept lay dormant until the 1950s, when John Archibald Wheeler revitalized the study of spacetime geometry, a field he dubbed "geometrodynamics." Wheeler was fascinated by the topological properties of spacetime and coined the term "wormhole" to describe the ER bridge.

However, Wheeler and his student Robert Fuller soon discovered a fatal flaw in the bridge as a means of transport. They analyzed the dynamics of the bridge and found that it is inherently unstable. In a dynamic universe, the throat of the wormhole opens and closes so rapidly that not even light can pass through it. Any attempt to traverse the bridge would result in the traveler being crushed by the collapsing throat, a singularity formed by the pinch-off event.

This discovery, known as the non-traversability of the Schwarzschild wormhole, seemed to close the book on the subject for practical physics. While later researchers like Kip Thorne and Michael Morris discovered that "exotic matter" (matter with negative energy density) could theoretically stabilize a wormhole, such matter has never been observed in sufficient quantities. The wormhole remained a topological curiosity, useful for thought experiments but irrelevant to the physical universe.

2.4 The 2026 Pivot: From Macroscopic to Microscopic

The research published in 2026 by Gaztañaga, Kumar, and Marto pivots back to Einstein and Rosen's original 1935 intent, but with a quantum twist. They argue that the focus on traversability—on sending spaceships or signals through the wormhole—was a distraction. The true purpose of the bridge, they contend, is not macroscopic transport, but microscopic consistency.³

The new study suggests that the ER bridge is not a structure that exists within spacetime, like a planet or a star, but is a fundamental feature of the fabric of spacetime itself. It serves as a connector between two distinct "arrows of time," a concept we will explore in depth. In this view, the "instability" that Wheeler identified is not a bug; it is a feature. The dynamic nature of the bridge is exactly what allows it to mediate the interactions of quantum fields in a universe that is expanding.⁴

3. The Quantum-Gravity Standoff

To understand why a reinterpretation of the wormhole is necessary, we must examine the "cold war" between the two pillars of modern physics: Quantum Mechanics (QM) and General Relativity (GR).

3.1 The Clash of Frameworks

Quantum Mechanics, specifically in the form of Quantum Field Theory (QFT), is the most precise theory humans have ever devised. It describes the behavior of subatomic particles with breathtaking accuracy. However, standard QFT is built on a specific stage: Minkowski spacetime. This is a "flat" spacetime where geometry is fixed and static. In Minkowski space, time is a universal parameter, ticking forward relentlessly. This allows physicists to define "positive energy" states and ensuring that probabilities always sum to 1 (unitarity).

General Relativity, conversely, describes gravity not as a force, but as the curvature of spacetime. In GR, spacetime is dynamic; it bends, warps, and stretches in response to mass and energy. There is no fixed background stage. Near a black hole, the concept of "time" becomes fluid. A second for an observer far away is not the same as a second for an observer falling in.

3.2 The Information Paradox

The conflict between these two frameworks reaches its breaking point at the event horizon of a black hole. In 1974, Stephen Hawking used a hybrid of QFT and GR to show that black holes are not truly black; they emit radiation (Hawking radiation) and eventually evaporate.

This discovery triggered the "Black Hole Information Paradox." In Quantum Mechanics, information is never destroyed. If you know the quantum state of a system today, you can theoretically reconstruct its past perfectly. This is the principle of Unitarity.

However, if a book falls into a black hole, and the black hole subsequently evaporates into a cloud of random thermal radiation, the information contained in the book appears to be erased from the universe. The final state (radiation) does not contain the information of the initial state (the book). This violates unitarity.

For fifty years, physicists have struggled to resolve this. Some suggested that information is destroyed (Hawking's original position). Others suggested it is hidden in the remnants of the black hole. Some even proposed "firewalls"—regions of intense energy at the horizon that incinerate anything before it enters, thereby preventing the paradox but violating the equivalence principle of GR.

3.3 The Failure of Standard QFT in Curved Space

The root of the problem, according to Gaztañaga and his colleagues, lies in how we apply Quantum Field Theory to curved spacetime. Standard QFT assumes a fixed arrow of time. It assumes that we can clearly distinguish between "past" and "future" and between "positive" and "negative" frequencies.

In the extreme curvature near a horizon, these distinctions blur. The "vacuum" state for one observer appears as a bath of hot particles for another (the Unruh effect). The 2026 report argues that trying to force the rigid, single-time-arrow framework of standard QFT onto the flexible geometry of a black hole is what leads to the paradox.¹¹

They propose that we need a new version of Quantum Field Theory—one that is natively designed to handle the symmetries of gravity. This is where Direct-Sum Quantum Field Theory (DQFT) enters the stage.

4. Direct-Sum Quantum Field Theory (DQFT): The Bifurcated Universe

The core innovation of the January 2026 report is the formal introduction of Direct-Sum Quantum Field Theory. This framework fundamentally alters the mathematical space in which the universe is defined.

4.1 Decomposing the Hilbert Space

In quantum mechanics, the state of a system is described by a vector in a mathematical space called a Hilbert space (H). In standard physics, we assume there is one single Hilbert space for the universe.

DQFT proposes that the total Hilbert space of reality is actually a Direct Sum of two orthogonal sectors. We can represent this descriptively as:

Total Reality = Universe Sector ⊕ Mirror Sector

Mathematically, this is written as H_Total = H₊⊕H_-¹⁰

• The Universe Sector (H₊): This is the reality we experience. It contains the standard particles and fields we observe. In this sector, the arrow of time points forward (entropy increases).

• The Mirror Sector (H_-): This is a parity-conjugate region. It is identical to our sector but inverted. In this sector, the microscopic arrow of time points backward relative to ours.

This decomposition is not an arbitrary addition. The researchers argue it is mandated by the underlying symmetries of spacetime. Gravity, in Einstein's formulation, is invariant under Time Reversal (T). If you play a movie of a planet orbiting a star backward, it still obeys the laws of gravity. However, standard Quantum Mechanics breaks this symmetry to define positive energy. DQFT restores the symmetry by explicitly including the time-reversed sector in the total description.¹⁰

4.2 The Bridge as a "Spacetime Mirror"

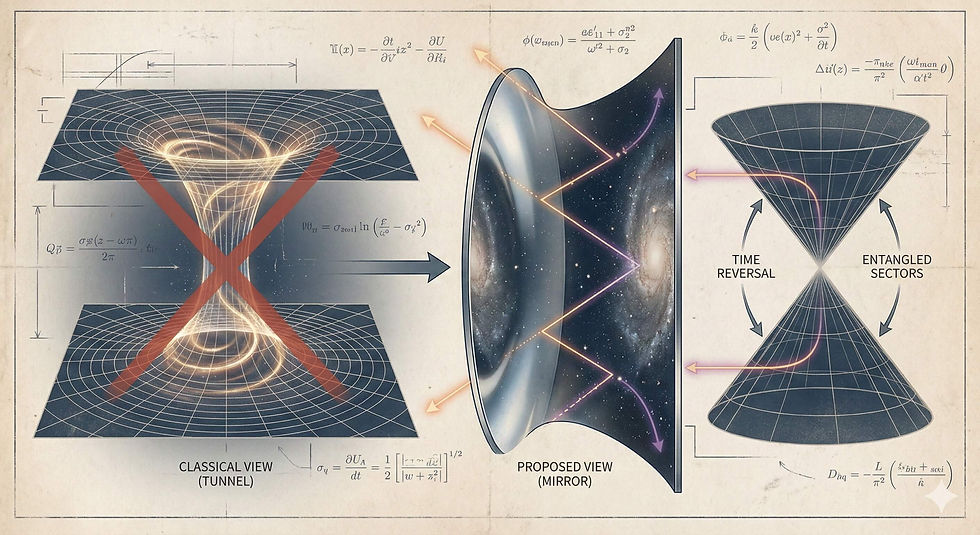
In this new context, the Einstein-Rosen bridge undergoes a dramatic transformation. It is no longer a tube connecting two distant points in space. Instead, it is the "plus" sign in the direct sum equation. It is the connection point, the "glue," between the Universe Sector and the Mirror Sector.¹

The researchers describe the bridge as a "Mirror in Spacetime".⁹ Imagine standing at the event horizon of a black hole. In classical GR, this is a point of no return. In DQFT, the horizon acts as a reflective surface for quantum information.

When a particle approaches the horizon, it interacts with this bridge. The information carried by the particle is not lost; rather, it is distributed across the two sectors. The "loss" of information in our sector (H⁺) is exactly compensated by a gain in the mirror sector (H_-). The "bridge" connects the microscopic arrow of time of the infalling particle with the microscopic arrow of time of a particle in the conjugate sector.³

4.3 Restoring Unitarity

This mechanism solves the Information Paradox by "balancing the ledger." If we look only at our sector (H₊), it appears that unitarity is violated—particles vanish into black holes, and information is lost. But this is because we are looking at only half of the system.

If we consider the total system (H₊ ⊕ H_-), the evolution is unitary. The information is preserved globally, even if it appears lost locally. The Einstein-Rosen bridge is the channel through which this unitarity is maintained, ensuring that the quantum books of the universe always balance.¹⁴

Table 1: Standard QFT vs. Direct-Sum QFT

Feature	Standard QFT (Curved Space)	Direct-Sum QFT (DQFT)
Hilbert Space	Single (H)	Split (H+ ⊕ H-)
Time Arrow	Fixed, Singular	Dual, Opposing Arrows
Horizon Physics	Information Paradox / Loss	Unitarity Restored via Mirroring
Role of ER Bridge	Geometric Curiosity / Wormhole	Fundamental Quantum Connector
Symmetry	Breaks Time-Reversal (T)	Preserves Global PT Symmetry

5. The Engine of Instability: The Inverted Harmonic Oscillator

One of the most technically rich and physically intuitive insights from the new report is the identification of the Inverted Harmonic Oscillator (IHO) as the fundamental dynamical system governing physics at horizons. To understand the bridge, one must understand the oscillator.⁴

5.1 The Valley and the Hill

The concept of the "Harmonic Oscillator" is the bedrock of physics. It describes any system that, when disturbed, wants to return to equilibrium.

• The Simple Harmonic Oscillator (SHO): Imagine a ball rolling at the bottom of a U-shaped valley. If you push it, it rolls up the side and then rolls back down, oscillating back and forth. This system is stable. It represents bound states, like an electron trapped in an atom, or a photon in a box. The mathematical potential is a parabola opening upward (V ∝+ x²).

• The Inverted Harmonic Oscillator (IHO): Now, imagine a ball balanced precariously at the very peak of an inverted U-shaped hill. If you push it even slightly, it does not oscillate. It rolls away, moving faster and faster. This system is unstable. The potential is a parabola opening downward (V ∝+ -x²).

In standard quantum mechanics, we almost always deal with the stable SHO. We model fields as collections of these stable oscillators.

5.2 Horizons are Inverted Oscillators

Gaztañaga and his team demonstrate that quantum fields near a horizon (whether a black hole horizon or the cosmological horizon of the expanding universe) behave like Inverted Harmonic Oscillators, not stable ones.¹⁶

This makes intuitive sense. A horizon is a place of instability. If you place a particle exactly at the horizon, it is balanced. If it moves slightly outward, it can escape to infinity. If it moves slightly inward, it falls into the singularity. It is exactly like the ball on the hill.

5.3 Phase Space Horizons and Quantum Chaos

The instability of the IHO creates a unique structure in "phase space"—the mathematical map of a particle's position and momentum.

• For a normal oscillator (the valley), the particle circles around the bottom. In phase space, the trajectory is a closed loop (a circle or ellipse).

• For an inverted oscillator (the hill), the particle flies away. In phase space, the trajectories are hyperbolas.

These hyperbolas define distinct regions in phase space that are separated by asymptotes. The researchers identified these asymptotes as "Horizons in Phase Space".¹⁸ They showed that these abstract mathematical boundaries in phase space are mathematically equivalent to the physical event horizons of black holes.

This is a profound unification. It suggests that the "event horizon" is not just a place in space, but a manifestation of the specific type of quantum instability characterized by the Inverted Harmonic Oscillator.

5.4 Scattering States and the Continuum

Unlike the stable oscillator, which has discrete energy levels (Ground state, Level 1, Level 2...), the IHO has a continuous spectrum of energy. It describes scattering—processes where particles come in, interact, and leave—rather than binding.

The "Bridge" in DQFT is effectively modeled by this IHO dynamics. The bridge connects the scattering states of the Universe Sector with the scattering states of the Mirror Sector. The "instability" of the IHO (the ball rolling away) corresponds to the information passing across the bridge into the other sector. The rate at which the ball rolls away (the Lyapunov exponent) is linked to the temperature of the black hole (Hawking temperature).⁵

6. The Mathematical Bridge: Riemann Zeros and Primes

Deepening the theoretical intrigue, the report connects the Inverted Harmonic Oscillator to one of the most famous unsolved problems in pure mathematics: the Riemann Hypothesis. This section explores how the physics of the wormhole may be encoded with the music of the primes.

6.1 The Riemann Hypothesis and Prime Numbers

The Riemann Zeta function (Z(s)) is a complex mathematical function that encodes the distribution of prime numbers (2, 3, 5, 7, 11...). In 1859, Bernhard Riemann hypothesized that all the "non-trivial zeros" of this function lie on a single vertical line in the complex plane (the critical line). If true, this implies a beautiful underlying order to the seemingly random distribution of primes.

For over a century, mathematicians have searched for a proof. In the early 20th century, the mathematician George Pólya and the physicist David Hilbert suggested a physical approach: perhaps the zeros of the Zeta function correspond to the energy levels (eigenvalues) of some unknown quantum mechanical system. If we could find a physical system whose energies are exactly the Riemann zeros, we would prove the hypothesis.

6.2 The Berry-Keating Conjecture

In 1999, physicists Michael Berry and Jon Keating made a specific conjecture. They proposed that the quantum system corresponding to the Riemann zeros is none other than the Inverted Harmonic Oscillator (specifically, a system with the Hamiltonian H = xp).⁴

However, there was a catch. For the Berry-Keating conjecture to work, the quantum system needed to possess specific discrete symmetries—specifically, it needed to respect Time Reversal in a way that standard quantum mechanics usually forbids.

6.3 Gravity Encodes Arithmetic

Gaztañaga’s team found that their DQFT framework—which naturally incorporates the IHO to describe gravity—possesses exactly the symmetry structure required by the Berry-Keating conjecture.

The "Direct Sum" of the two time-reversed universes provides the necessary mathematical space for the Berry-Keating Hamiltonian to be fully realized.⁴ This suggests a startling "trinity" in physics:

1. Gravity (Spacetime Curvature/Horizons)

2. Quantum Mechanics (IHO Dynamics)

3. Number Theory (Prime Numbers/Riemann Zeros)

The implication is that the Einstein-Rosen bridge is not just a physical structure but a realization of a deep mathematical unity. The chaotic scattering of the IHO (gravity) encodes the fundamental order of arithmetic (primes). The "Mirror in the Void" reflects not just the other side of time, but the deepest structures of mathematics itself.²¹

7. Observational Evidence: The Cosmic Microwave Background

Theoretical frameworks, no matter how elegant, require empirical evidence to move from philosophy to science. The most explosive aspect of the January 2026 report is the claim that this "Mirror Universe" model resolves decades-old anomalies in the Cosmic Microwave Background (CMB).⁶

7.1 The Standard Model of Cosmology (λ CDM)

The current ruling paradigm of cosmology is the λ CDM model, supplemented by the theory of Inflation. Inflation posits that the universe underwent a period of exponential expansion in the first fraction of a second. This expansion smoothed out the universe, making it isotropic (looking the same in all directions) and homogeneous.

According to standard inflation, the seeds of galaxies were microscopic quantum fluctuations that got stretched to cosmic sizes. These fluctuations should be Gaussian random noise. There should be no preferred direction, no special axis, and no correlation between widely separated points on the sky (other than the standard acoustic scale).

7.2 The Anomalies

However, when satellites like WMAP and Planck mapped the CMB in high detail, they found "anomalies" that refused to go away.

• The Cold Spot: A massive region of the southern sky (spanning roughly 10 degrees) is significantly colder than standard theory allows. The probability of this happening by chance is extremely low (<1%).²³

• Hemispherical Power Asymmetry: The universe appears to be "lopsided." One hemisphere of the sky has slightly stronger fluctuations than the other.

• The Low Quadrupole: The largest-scale fluctuations (the "bass notes" of the universe) are much quieter than predicted.

For twenty years, the consensus was to dismiss these as statistical flukes or "look-elsewhere" effects. But they persisted across different satellites and different frequencies.

7.3 The New Analysis: Parity Asymmetry

Gaztañaga, Kumar, and Marto re-analyzed the Planck data looking specifically for signatures of the Direct-Sum model.

If the universe is a direct sum of two parity-conjugate sectors (H₊ ⊕ H_-), then the fluctuations in our universe should be entangled with the fluctuations in the mirror universe. This entanglement should manifest as a specific type of symmetry breaking: Parity Asymmetry.

The Finding: They discovered a strong "Antipodal Anti-Correlation."

Imagine a point on the sky (Coordinate A). Now look at the point exactly opposite to it on the celestial sphere (Coordinate B, the antipode).

• Standard Theory says: A and B should be uncorrelated. Whether A is hot or cold tells you nothing about B (once you subtract the dipole).

• Direct-Sum Theory says: If A is a hot spot, B is highly likely to be a cold spot (and vice versa). The universe acts like a mirror.

The researchers found that this anti-correlation exists and is statistically robust. Specifically, the "odd" parity modes (patterns that flip sign when reflected) are dominant over the "even" modes at large scales.

7.4 The 650x Statistical Significance

To quantify this, the researchers used Bayesian statistics. They compared the probability of the data given the Standard Inflation model versus the Direct-Sum Inflation (DSI) model.

The result was staggering. The Direct-Sum model is 650 times more likely to produce the observed CMB data than the standard inflationary model.⁶

This is a massive Bayes factor. In statistical terms, it is "decisive" evidence. It suggests that the "anomalies" like the Cold Spot are not flukes; they are the fingerprints of the mirror universe. The Cold Spot is effectively the "shadow" cast by the entanglement with the time-reversed sector.²⁴

Table 2: Comparison of Cosmological Models

Feature	Standard Inflation (SI)	Direct-Sum Inflation (DSI)
Foundational Basis	Single Field, Single Hilbert Space	Direct Sum (H+ ⊕ H-)
Symmetry Assumption	Assumes Isotropy & Homogeneity	Enforces Parity (P) & Time (T) Symmetry
Microscopic Time	Fixed forward arrow	Two opposing microscopic arrows
CMB Predictions	Scale-invariant, Gaussian noise	Parity Asymmetric, Antipodal correlations
Anomalies (e.g. Cold Spot)	Unexplained (Statistical Flukes)	Predicted Consequences of Unitarity
Statistical Evidence	Baseline (1x)	650x stronger evidence 22

8. Reinterpreting ER=EPR

The findings of this report also force a re-evaluation of one of the most trendy ideas in theoretical physics: the ER=EPR conjecture.

8.1 The Maldacena-Susskind Conjecture

Proposed by Juan Maldacena and Leonard Susskind in 2013, ER=EPR suggests a duality between entanglement and wormholes.

• ER refers to the Einstein-Rosen bridge (geometric connection).

• EPR refers to the Einstein-Podolsky-Rosen paradox (quantum entanglement).

The conjecture states that any two entangled particles are connected by a microscopic wormhole. If you entangle two black holes, they form a wormhole between them.

8.2 The New Horizon-Local View

The 2026 report refines this idea. The original ER=EPR was largely holographic, often visualized as a physical tunnel connecting distinct regions. The DQFT framework reinterprets the "bridge" as a Superselection Sector Connection.

In this view, the "wormhole" is not a spatial tunnel that threads through the bulk of spacetime. Instead, it is a "horizon-local" phenomenon. The entanglement (EPR) is the result of the direct-sum structure. The "wormhole" (ER) is the mathematical operation that "glues" the Universe Sector to the Mirror Sector at the horizon.¹¹

This means that spacetime connectivity is not about tubes stretching across the universe, but about the way quantum fields are sewn together at their boundaries (horizons). The "bridge" is the stitching.

9. Philosophical and Physical Implications

The ramifications of this report extend far beyond the technical details of black holes and the CMB. They touch on the very origin of the universe and the nature of reality itself.

9.1 The Big Bounce vs. The Big Bang

If the universe is composed of two time-reversed sectors, the Big Bang may not be a beginning in the traditional sense. The standard Big Bang theory suffers from the "initial singularity" problem—a moment t=0 where physics breaks down (much like the black hole singularity).

The Direct-Sum model supports the concept of a "Big Bounce." The snippets allude to "Gravitational Bounce from the Quantum Exclusion Principle".²² In this scenario, the universe existed prior to the Big Bang in a contracting phase. It shrank down to a minimal size (the "bridge") and then "bounced" outward, splitting into the two sectors (H₊ ⊕ H_-).

The "mirror" sector acts as a thermodynamic counterweight. As entropy increases in our forward-time universe, it also increases in the backward-time mirror universe. From a global perspective, the "book" of the universe stays balanced.³

9.2 The Nature of Time

Perhaps the most unsettling implication is for our perception of time. We perceive time as flowing inexorably from past to future. But DQFT suggests that deep down, at the fundamental level of quantum fields and gravity, time is bidirectional.

The "microscopic arrows of time" are symmetric. Our macroscopic experience of a "forward" flow is a result of being trapped in one sector (H₊) of the direct sum. The "Mirror Universe" is not a sci-fi parallel dimension where we have evil goatees; it is a necessary mathematical partner that allows our timeline to exist consistently with the laws of quantum mechanics.

9.3 Why We Don't See Wormholes

Finally, this explains why we haven't found physical wormholes (like the one in Interstellar) despite looking for them.

Wormholes "may not exist" as macroscopic tunnels for spaceships because they are fundamental microscopic structures. They are the "pixels" of spacetime connectivity, not the "pipes." They are everywhere—knitting together the fabric of reality and time—but they are not traversable passages in the classical sense. We cannot fly through them, but we exist because of them.1

10. Conclusion: The Universe in the Mirror

The research published in January 2026 by Gaztañaga, Kumar, and Marto marks a potential paradigm shift in theoretical physics. By revisiting the original 1935 Einstein-Rosen bridge, they have stripped away decades of science fiction accumulation to reveal a starker, more profound truth. The "wormhole" is a mathematical necessity—a mirror in spacetime that balances the quantum books of the universe.

The evidence is not just in the equations; it is written on the sky. The 650-fold statistical preference for this model in the Cosmic Microwave Background suggests that the anomalies physicists have puzzled over for twenty years were actually signals. They were the fingerprints of the "mirror universe," the antipodal reflection of our own reality, connected to us by the microscopic bridges that Einstein and Rosen conceived of nearly a century ago.

We may not be able to travel through these wormholes to distant galaxies. But in a deeper sense, we are already traveling through them. Every moment of time, every interaction of a quantum field, is sustained by this hidden architecture—a bridge over the void, reflecting the universe back at itself. As we gaze into the deepest past of the cosmos, we are finding that the universe is not a lonely, expanding bubble, but a paired, symmetric dance of time and anti-time.

Works cited

1. Wormholes may not exist—we've found they reveal something ..., accessed January 16, 2026, https://phys.org/visualstories/2026-01-wormholes-weve-reveal-deeper-universe.amp

2. Enrique Gaztanaga (0000-0001-9632-0815) - ORCID, accessed January 16, 2026, https://orcid.org/0000-0001-9632-0815

3. Wormholes Reveal Something Deeper About Time and the Universe - RealClearScience, accessed January 16, 2026, https://www.realclearscience.com/articles/2026/01/16/wormholes_reveal_something_deeper_about_time_and_the_universe_1159162.html

4. Einstein-Rosen Bridges: A Quantum Connection to Prime Numbers - Dark Cosmos, accessed January 16, 2026, https://darkcosmos.com/home/f/einstein-rosen-bridges-a-quantum-connection-to-prime-numbers

5. Quantum Inverted Harmonic Oscillator - Emergent Mind, accessed January 16, 2026, https://www.emergentmind.com/topics/quantum-inverted-harmonic-oscillators

6. Prof. Enrique Gaztanaga | Author | Institute of Cosmology and Gravitation, University of Portsmouth, Portsmouth, UK - SciProfiles, accessed January 16, 2026, https://sciprofiles.com/profile/gaztanaga

7. [2512.20691] A new understanding of Einstein-Rosen bridges - arXiv, accessed January 16, 2026, https://arxiv.org/abs/2512.20691

8. Physicist proves wormhole travel is possible, but it's not what you think - Silicon Republic, accessed January 16, 2026, https://www.siliconrepublic.com/innovation/wormhole-travel-possible

9. Wormholes may not exist – we've found they reveal something deeper about time and the universe : r/STEW_ScTecEngWorld - Reddit, accessed January 16, 2026, https://www.reddit.com/r/STEW_ScTecEngWorld/comments/1qeqj6z/wormholes_may_not_exist_weve_found_they_reveal/

10. Towards a Unitary Formulation of Quantum Field Theory in Curved Spacetime: The Case of de Sitter Spacetime - MDPI, accessed January 16, 2026, https://www.mdpi.com/2073-8994/17/1/29

11. A new understanding of Einstein-Rosen bridges - arXiv, accessed January 16, 2026, https://arxiv.org/html/2512.20691v1

12. Revisiting Quantum Field Theory in Rindler Spacetime with Superselection Rules | University of Portsmouth, accessed January 16, 2026, https://pure.port.ac.uk/ws/portalfiles/portal/98188709/Revisiting_Quantum_Field_Theory_in_Rindler_Spacetime_with_Superselection_Rules.pdf

13. Direct-Sum Quantum Theory - Emergent Mind, accessed January 16, 2026, https://www.emergentmind.com/topics/direct-sum-quantum-theory

14. CMB Parity Asymmetry from Unitary Quantum Gravitational Physics - ResearchGate, accessed January 16, 2026, https://www.researchgate.net/publication/393427948_CMB_Parity_Asymmetry_from_Unitary_Quantum_Gravitational_Physics

15. Revisiting Quantum Field Theory in Rindler Spacetime with Superselection Rules - MDPI, accessed January 16, 2026, https://www.mdpi.com/2218-1997/10/8/320

16. The logarithmic phase singularity in the inverted harmonic oscillator | AVS Quantum Science, accessed January 16, 2026, https://pubs.aip.org/avs/aqs/article/4/2/024402/2835230/The-logarithmic-phase-singularity-in-the-inverted

17. Duality between the quantum inverted harmonic oscillator and inverse square potentials, accessed January 16, 2026, https://arxiv.org/html/2402.13909v1

18. The logarithmic phase singularity in the inverted harmonic oscillator, accessed January 16, 2026, https://elib.dlr.de/186073/2/5.0074429.pdf

19. The Riemann Zeros as Spectrum and the Riemann Hypothesis - MDPI, accessed January 16, 2026, https://www.mdpi.com/2073-8994/11/4/494

20. Quantum mechanics: The nontrivial zeros of the Riemann zeta function interpreted as a spectrum of energy levels, accessed January 16, 2026, https://empslocal.ex.ac.uk/people/staff/mrwatkin/zeta/physics1.htm

21. R. Bhaduri, et. al. - The Riemann zeta function and the inverted harmonic oscillator, accessed January 16, 2026, https://empslocal.ex.ac.uk/people/staff/mrwatkin/zeta/harmonic.htm

22. Enrique Gaztañaga's research works | University of Portsmouth and other places, accessed January 16, 2026, https://www.researchgate.net/scientific-contributions/Enrique-Gaztanaga-2294600780

23. A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions a - Università di Bologna, accessed January 16, 2026, https://cris.unibo.it/retrieve/1b3da091-b1fc-434a-bc59-6bacb48aac00/1-s2.0-S2214404822000179-main.pdf

24. A new understanding of Einstein-Rosen bridges - arXiv, accessed January 16, 2026, https://arxiv.org/html/2512.20691v2

25. Finding origins of CMB anomalies in the inflationary quantum fluctuations - University of Portsmouth, accessed January 16, 2026, https://pure.port.ac.uk/ws/portalfiles/portal/91029653/Finding_origins_of_CMB_anomalies_in_the_inflationary_quantum_fluctuations.pdf